순열

들어가기 전에..

- 경우의 수

여러 개의 사건이 일어날 때 경우의 수를 따지는 방법. 조합론에서 다루는 수많은 논의를 가능케하는 가장 기본적인 두 원리.

• 합의 법칙: 경우의 수를 구해야 할 여러 사건들이 영향을 주거나 일어나는 상황의 구조가 닮지 않은 다른 경우, 경우의 수를 쪼개서 계산하게 된다. or이 합의 법칙이다.
  두 사건 A, B의 경우의 수를 따진다면, 사건 A가 일어나는 경우의 수가 m가지, 사건 B가 일어나는 경우의 수는 n가지라면 A와 B 어느 쪽이 일어나는 경우의 수는 m + n 가지다. '또는', '~이거나'라는 표현을 사용한다면 합의 법칙 문제이다.
• 곱의 법칙: 경우의 수를 구해야 할 여러 사건들이 서로 영향을 주지 않거나 일어나는 상황이 구조가 닮은 경우, 경우의 수를 뭉쳐서 계산하게 된다. and가 곱의 법칙이다.
  두 사건 A, B의 경우의 수를 따진다면, 사건 A가 일어나는 경우의 수가 m가지, 사건 B가 일어나는 경우의 수는 n가지라면 A와 B가 동시에 일어나는 경우의 수는 m×n 가지다.

합의 법칙은 주사위의 눈이 2 또는 5가 나올 경우의 수를 생각하면 된다. 주사위의 눈이 2 또는 5가 나오면 되므로 2가 나올 경우의 수 1가지와 5가 나올 경우의 수 1가지를 더하여 2가지가 나온다. 1+1=21+1=2

곱의 법칙은 주사위를 두 번 던져 처음엔 짝수가 나오고 그 다음 홀수가 나올 경우의 수를 생각하면 된다. 처음에 짝수가 나올 경우의 수 3가지(2, 4, 6)에 두번째 홀수가 나올 경우의 수 3가지(1, 3, 5)를 곱하면 9가지이다. 3×3=93×3=9

그런데 이 두 가지를 구분하는 부분에서 많이 헷갈리게 되는데, 간단히 말해 사건과 사건이 이전의 결과에 영향을 받거나 관계가 서로 엮여있을 때 합의 법칙을 사용하고, 영향을 받지 않는 독립적인 사건이라면 곱의 법칙을 사용하면 된다. '동시성'이라는 단어가 애매한 것이, 예를 들어 3개의 갈림길을 지나 다시 2개의 갈림길중 하나를 선택하는 문제라면, 분명 동시에 일어나는 사건은 아니지만 곱의 법칙을 사용해야 한다. 어떤 두 사건이 즉 동시에 일어날 경우 곱의 법칙을 쓰지만(동시에 일어나지만 합의 법칙을 쓰는 경우는 없으므로) 곱의 법칙을 쓴다고 해서 어떤 두 사건이 항상 동시에 일어나는 것은 아니다.정 모르겠다면 문제에서 숫자를 줄여서 상상해보자. EBS강좌에서 한 강사는 동시성의 혼란을 방지하고자 '잇달아'라는 개념을 도입하면 이해하기 쉽다고 하니 참고할 것.어디까지나 캐바케지만 이런 연습을 여러번 거치다 보면 자유자재로 두 법칙을 사용하게 될 것이다.

고등학교 과정에서 법칙이란 이름을 붙이기 부끄러운 간단한 내용에 다짜고짜 '법칙'인가 싶지만 공부를 깊이 하면 결국 순열과 조합의 기술적인 부분을 제치고 결정적으로 중요한 내용이라는 것을 깨달을 수 있다. 문제를 풀 때 흔히 쓰는 공식과 기술은 고난도 문제가 다루는 변태적으로 특수한 상황에서는 결국 상황을 많이 복잡하게 만들 뿐이다. 결국엔 상황을 최대한 단순화시킨 후 각각의 케이스에 대해서 곱의 법칙으로 뭉친 항들을 곱하는 것이나, 상황이 여의치 않거나 단순하게 해결할 수 있다면 합의 법칙으로 해결하는 것도 나쁘지 않다.

기호로 간단하게 n!로 나타내며 1부터 n까지의 자연수를 모두 곱하는 것을 의미한다. 팩토리얼이라고도 불린다.

출처:나무위키

 

 

순열이란

서로다른 n개에서 r(0<r≤n)개를 택하여

일렬로 나열하는 것을

n개에서 r개를 택하는 순열이라 한다.

 식으로 표현하면 이렇다.

 

첫 번째 순열은 원순열

 

말그대로 원으로 배열하는 것인데 그림으로 보면 이렇다

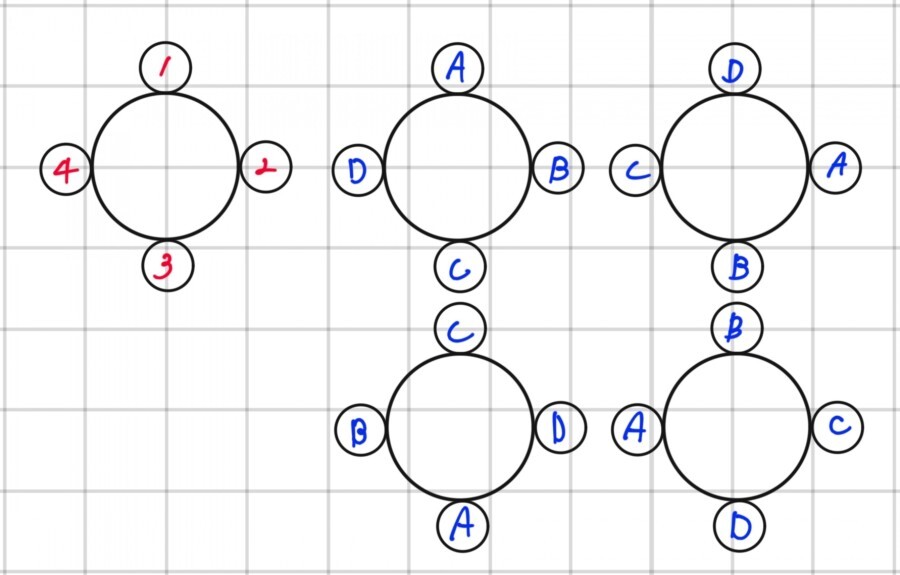
위 사진과 같이 A, B, C, D를 배치시키는데

원형 탁자에 배열 시킨다면

위 네가지 경우가 똑같은 경우라고 할 수 있다

항상 A의 좌우측에는 B와 D가 배치되어 있고,

B,C,D 좌우측에도 변화가 없다.

그렇기에 4가지 경우는 같은 경우.

 

그럼 우리가 처음 배웠던 순열로 보면

4명을 일렬로 세우는 방법의 수는 4! 이지만

원형탁자에 배열 한다면 서로 같은 경우가 4가지씩 있으므로

확장해서 서로 다른 n개를 원형탁자에 배열한다고 하면

원순열의 수는

 

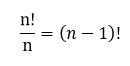
Q1. 원형 탁자에 A, B, C, D, E가 둘러 앉을 때 다음을 구하시오.

(1) 6명이 앉는 모든 경우의 수

(2) A, B가 이웃하여 앉는 모든 경우의 수

(3) D, E가 마주 보고 앉는 모든 경우의 수

 

두 번째 순열은 중복순열.

 

중복순열이란

서로 다른 n개에서 중복을 허용하여

r개를 택하여 일렬로 배열하는 것을

n개에서 r개를 택하는 중복순열이라 한다.

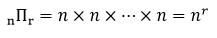
중복순열은 위와 같이 표현하는데,

중복을 허용하기 때문에

첫 번째 자리에 올 수 있는 경우의 수도 n,

두 번째 자리에 올 수 있는 경우의 수도 n,

계속해서 r번째 자리에 올 수 있는 경우의 수 또한 n개다.

 

Q2. 비밀번호를 만들 때 0부터 9까지의 번호를 사용할 수 있으며,

    비밀번호는 총 5개의 숫자로 이루어져 있다.

    만들 수 있는 비밀번호의 개수를 구하시오.

 

세 번째 순열은 중복순열이라고도 하는데,

같은 것이 있는 순열의 수를 구하는 경우.

 

만약 파란색 카드 2장과 빨간색 카드 3장이 있는데,

이 카드 5장을 일렬로 줄 세우는 방법은 당연히

5!.

 

하지만 같은 색끼리 카드는 구별이 불가능 하다면?

파란색 카드 2장끼리 순서가 바뀌는 경우 2!과

빨간색 카드 3장끼리 순서가 바뀌는 경우 3!만큼

나누어 주게되면 그 답을 쉽게 구할 수 있다?

 

정리하자면

 

 

출처 :https://mathmen.tistory.com/11